熱音響FAQ
熱音響デバイスに関してよくある質問とその答えをまとめました.もっと知りたい場合は,専門の教科書や論文を読んでみたり,こちらに質問を寄せてください.
(2021年10月に質問と回答を追加しました.) Q1. 熱音響デバイスにはどんな種類がありますか?
Q2. 熱音響デバイスでは熱流と仕事流の間でエネルギー変換が起こると聞きました.
熱流と仕事流について教えてください.
Q3. 熱音響デバイスで起こるエネルギー変換にとって大事な物理量は何ですか?
Q4. 熱音響デバイスの利点は何ですか?
Q5. 音波のパワー(音響パワー)は小さいのでは?
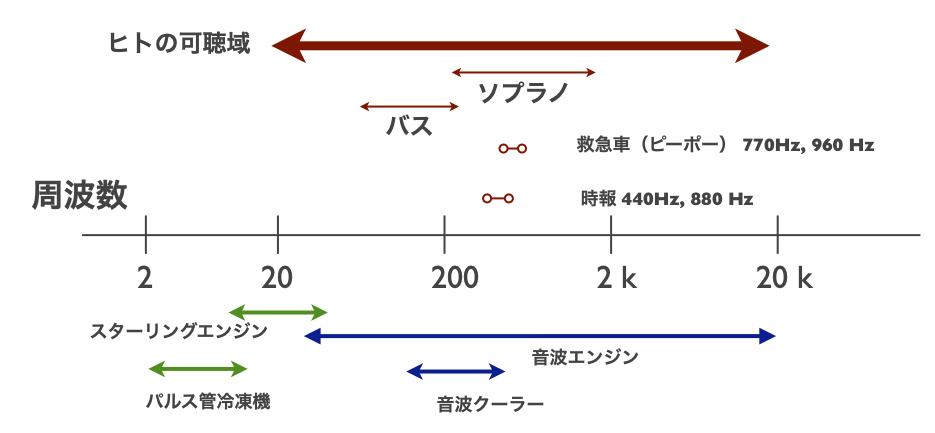
Q6. 音の周波数範囲は20 Hz 〜 20 kHzと聞いたことがあります.
この周波数範囲と音波エンジンの動作周波数は関係ありますか?
Q7. 音波エンジンには共鳴管とループ管のタイプがあるようですが,ほかにもありますか?
Q8. 音波エンジンはどのようにしてひとりでに振動を開始するのですか?
Q9. どれだけの温度差があれば音波エンジンは動作しますか?
Q10. 音波エンジン,音波クーラーの応用先は?
Q11. 音波エンジンを応用して発電機を作ることはできますか?
Q12. 音波による冷却作用が起こる仕組みは何ですか?
Q13. スターリングエンジンと音波エンジンは同じ原理で動作するのですか?
Q14. 音波エンジンや音波クーラーは実用化されるのでしょうか?
Q15. エンジンやクーラー以外にも面白い熱音響現象はありますか?
Q16. 熱音響デバイスについてもう少し勉強してみたくなりました.
参考になる本や解説論文はありますか?
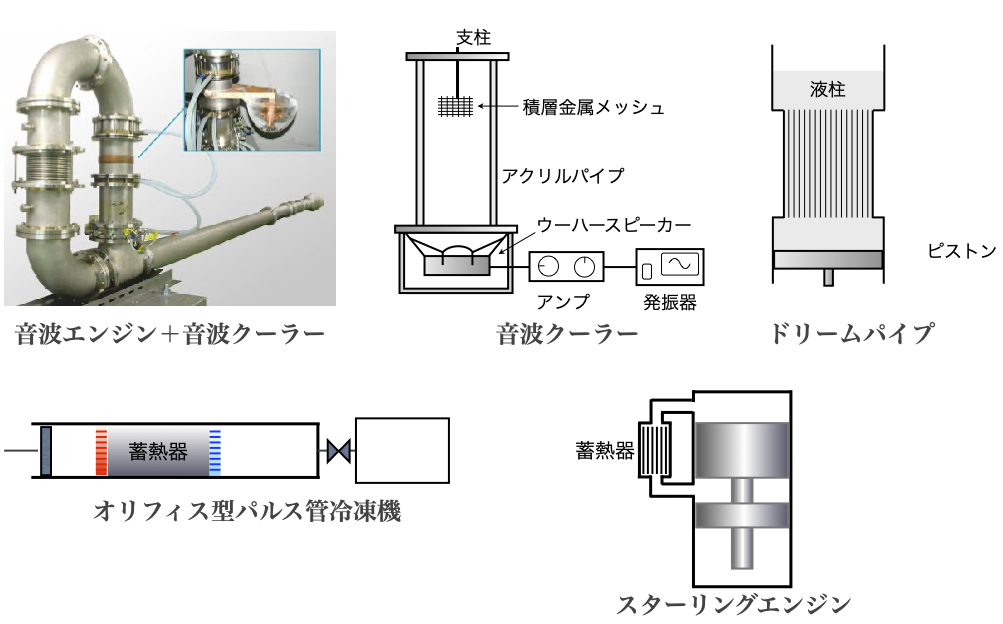
気体や液体の振動流れを使って熱輸送やエネルギー変換を行うデバイスを広く熱音響デバイスと呼ぶとすると,多様な種類が存在します.
外部からの熱入力の一部を仕事に変換する「原動機」には,音波エンジンやスターリングエンジンがあります.音波エンジンの出力する仕事は音響パワーですが,スターリングエンジンの出力する仕事は機械的な動力という点が異なります.
外部からの仕事を使って低温から高温への熱輸送を行う「クーラー」には,音波クーラーやスターリングクーラーがあります.音波クーラーは音響パワーが動力源ですが,スターリングクーラーは機械的動力が動力源です.スターリングクーラーの仲間にはパルス管冷凍機もあります.
振動流れを使って高温から低温への熱輸送を促進するデバイスはドリームパイプです.流体の変位振動の振幅と周波数で,熱輸送能力は大きく変化します.クーラーが環境温度より冷却することを目的とすることが多いのに対し,ドリームパイプは環境温度まで放熱することに適したデバイスです.
以上の原動機,クーラー,ドリームパイプを組み合わせたデバイスも可能です.エンジンとクーラーを接続すれば,熱入力により低温生成を行うことができます.原動機とドリームパイプを組み合わせれば自励振動式のヒートパイプになります.
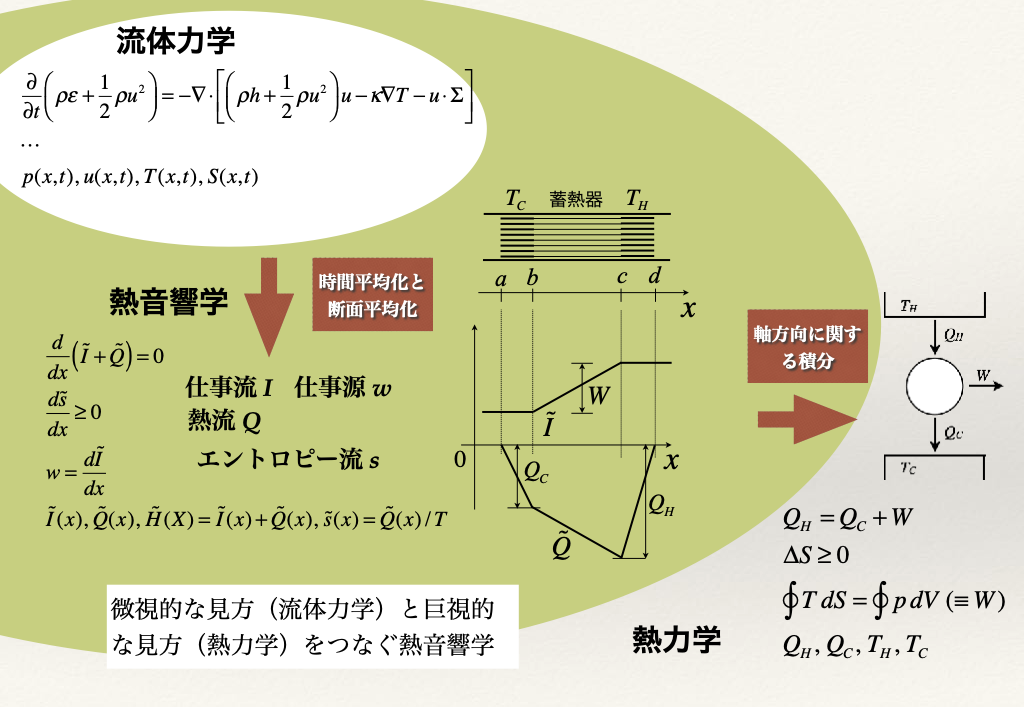
熱力学でエネルギー変換を言うときには,熱と仕事の間の相互変換を指します.ちなみに熱も仕事もエネルギー移動の形態ですが,熱はエントロピーに関係しているのに対し,仕事は全く無関係であるという大きな違いがあります.熱音響デバイスの場合には,管路内の流体の振動運動に伴う「熱」と「仕事」について考える必要があります.
富永昭氏や米国ロスアラモス研究所のWheatleyはそれぞれ独立に流体力学の基礎方程式に基づいて,流体の振動運動によって輸送されるエネルギーの流れを検討し,実質的には流体のエンタルピー流を考えればよいこと,さらにはエンタルピー流を流体のエントロピーに関係した成分(熱流)と無関係な成分(仕事流)に分解しました.
単位断面積あたりの流体のエンタルピー流束密度\( H \)は,流体の密度\(\rho_m \)(ある位置を中心に振動する流体の時間的平均密度),エンタルピーの時間的平均値からのずれ\(h'\),管軸方向の流速振動\(u' \)の積の1周期にわたる時間平均と断面に関する平均として次のように書けます. $$ H = \rho_m \langle \langle h'u' \rangle \rangle $$ ここで,\(\langle \langle ~ \rangle \rangle\)は内部の量の時間平均と断面平均をとる演算を表します. \( h'\)は平均値からのずれなので,比較的小さい場合には\( h'=T_mS'+V_mp'\)のようにエントロピーの時間平均からのずれ\(S'\)と圧力の時間平均からのずれ\(p'\)で展開することができます.なお\(T_m\)は時間平均温度,\(V_m \)は時間平均体積です.(通常の熱力学の記法では\(dH = TdS+Vdp \)です)これを代入すると,\( H = \rho_mT_m \langle \langle S' u' \rangle \rangle +\langle \langle p'u' \rangle \rangle \)となります.熱流\(Q \)が\(Q= \rho_mT_m \langle \langle S' u' \rangle \rangle\),仕事流\(I \)が\(I =\langle \langle p'u' \rangle \rangle\)です.なお仕事流は音響学では音響強度と呼ばれています.
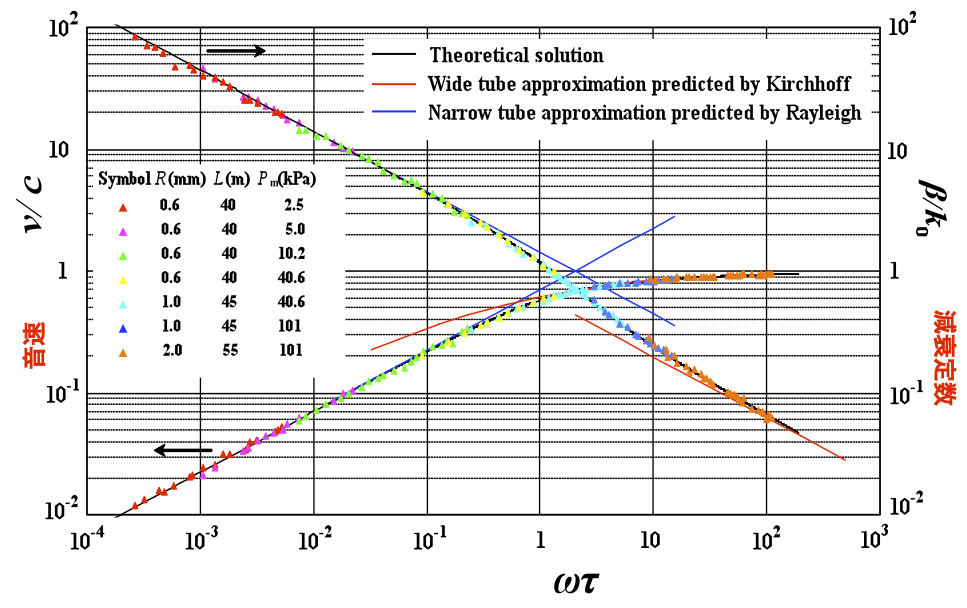
熱音響デバイスでエネルギー変換が起こるのは,蓄熱器やスタックと呼ばれる狭い流路の集合体です.この流路壁と熱交換しながら往復運動することでエネルギー変換が生じます.
熱交換できるかどうかの目安が流体の振動運動の角振動数\( \omega \)と熱緩和時間と呼ばれる特徴時間\(\tau_\alpha\)の積\( \omega \tau_\alpha \)です.熱緩和時間\(\tau_\alpha\)は流体の熱拡散係数\(\alpha\) [\(=\kappa/(\rho C_p)\)]と流路半径\( r \)を用いて\(\tau_\alpha =2\alpha/r^2 \)と書けます.積\( \omega \tau_\alpha \)が\( \omega \tau_\alpha \gg 1\)ならば流体の振動運動は断熱的でエネルギー変換は期待できません.\( \omega \tau_\alpha \ll 1 \)ならば流体は等温的な熱交換をしながら振動運動することになりますが,粘性によるエネルギーロスが問題になることがあります.\( \omega \tau_\alpha \sim 1 \)ならば,熱交換しながらも粘性によるロスも比較的小さくなります.結果的に多くの熱音響デバイスの蓄熱器やスタックでは,\( \omega \tau_\alpha \)の値は0.05から20程度になっています. 図に示したのは管内音波の音速と減衰定数です.横軸は\( \omega \tau_\alpha \)です.管半径と作動気体(乾燥空気)の充填圧力がさまざまに変化しても,音速と減衰定数のデータはそれぞれ共通の曲線を呈します.このことは\( \omega \tau_\alpha \)が管内音波を記述するよい物理量であることを表しています.
流体の振動運動を特徴付けるのが圧力振動と流速振動の間の位相差\( \phi \)と振幅比\(z\)です.スターリングエンジンで目指すのは,位相差は同位相,また流速振幅に対して圧力振幅が大きいことです.大きさの目安となるのは作動気体の特性インピーダンスです.特性インピーダンスは作動気体の密度\(\rho\)と音速\(c\)の積で与えられます.効率のよい音波エンジンでは振幅比は\( z \sim\) 30\(\rho c \)程度と報告されています.どの程度の\( z \)が最適化は,温度勾配の大きさや\( \omega \tau_\alpha \)の値も関係するので,一概には言えませんが,参考になる値です.
\( \omega \tau_\alpha \)が十分に小さく,また\(\phi \sim 0 \)でしかも\(z \)が大きければ粘性によるロスを小さく保ったままスターリングサイクルが行われ,本質的に高い効率が期待されます.スターリングエンジンではピストンやディスプレーサーの振動運動を機械的に制御して,そのような流体の振動運動を作り出します.音波エンジンでは,ループ管の適切な位置に蓄熱器を設置することで,自動的に望みの振動運動が実現できます.
熱音響デバイスの音波エンジンや音波クーラーは,ピストンの代わりに音波(気体の振動運動)を用います.そのため,機械的な可動部品を持たず,構造が著しく簡単です.パイプや金属メッシュだけで構成され,特殊な材料や加工も不要です.
熱音響デバイスはいずれも作動気体として使用するのはヘリウムやアルゴンなどの不活性ガスです.低コスト化を目指す場合には,単に空気を作動気体として使用することもあります.フロンガスや代替フロンガスは不要です.
現在の熱機関が複雑な形状をしていることに比べると,圧倒的に単純なのが特徴的です.音波エンジンの面白いところは,性能が向上するきっかけとなったのは,直線上の配管(共鳴管)をループ状にしたこと(ループ管)や蓄熱器の個数を1つではなくて複数にしたことなどの,単純な工夫だったことです.簡単な構造を維持したままで性能向上させる工夫はあとから見れば簡単なのですが,すぐにはなかなか思いつきません.単純構造を維持したままエネルギー変換技術として発展させるのは,挑戦しがいのあるテーマです.
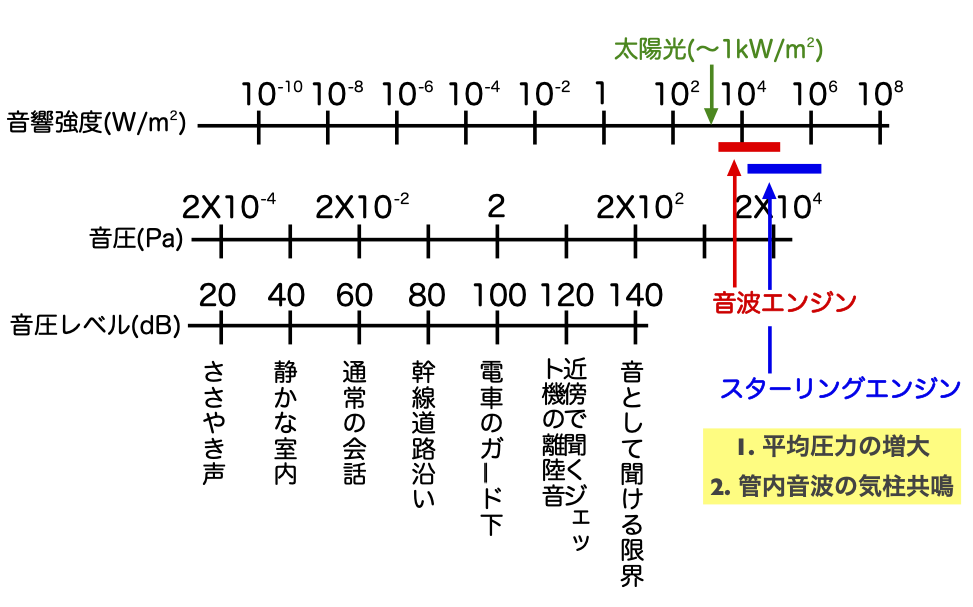
日常生活で経験する音では,その圧力振幅レベルはせいぜい1 Pa程度ですから,それに伴う音響パワーもかなり小さくなります.大気圧,室温の空気を仮定すれば,その特性音響インピーダンスは410 Pa•s/m程度なので,流速振幅はおよそ2.4 mm/sです.進行波の場合は音響強度は圧力振幅と流速振幅の積の半分ですから,1.2 mW/m\(^2\)です.1m\(^2\)というと傘を広げた程度の面積ですから,そこを通過する音響パワーが1.2 mWというのは確かにエンジンとしてみれば頼りないかもしれません.ちなみに地表に降り注ぐ太陽光のエネルギー流速は1 kW/m\(^2\)程度と言われていますが,これに比べても著しく小さな値です.
熱音響デバイスでは,管内に充填した加圧気体を作動流体としています.また共鳴現象をつかうことで,圧力振幅のレベルは充填圧力の10%程度になります(音波エンジン).結果的に音波エンジンでは10\(^5\) W/m\(^2\)程度の音響強度が可能です.スターリングエンジンのようにピストンを使えばもっと大きな圧力振幅レベルを実現することができます.音響パワーだからといって決して小さくありません.
この周波数範囲と音波エンジンの動作周波数は関係ありますか?
本質的には関係ありません.音波エンジンにとって大事なのは,振動流体が蓄熱器やスタックを構成する流路壁と十分に熱交換できることです.周波数が高ければ狭い流路を用いればよいし,周波数が低ければ比較的広い流路でも十分ということになります.ヒトにとって音として聞こえるかどうかと,エネルギー輸送,エネルギー変換が可能かは別問題です.
スターリングエンジンやパルス管冷凍機では,2 Hzから20 Hz程度の周波数で動作します.もはやヒトには「音」としては知覚できない周波数領域ですが,圧力振動を伴う流体の振動運動が鍵となる点では,音波エンジンや音波クーラーと本質的に同等なエネルギー変換デバイスです.
いずれの装置も圧力振幅の値を見れば大音響なので,熱音響デバイスはうるさいと考えるのは早合点です.なぜなら,密閉された管内での大振幅音波だからです.実際,スターリングエンジンは静粛なエンジンの代表例です.
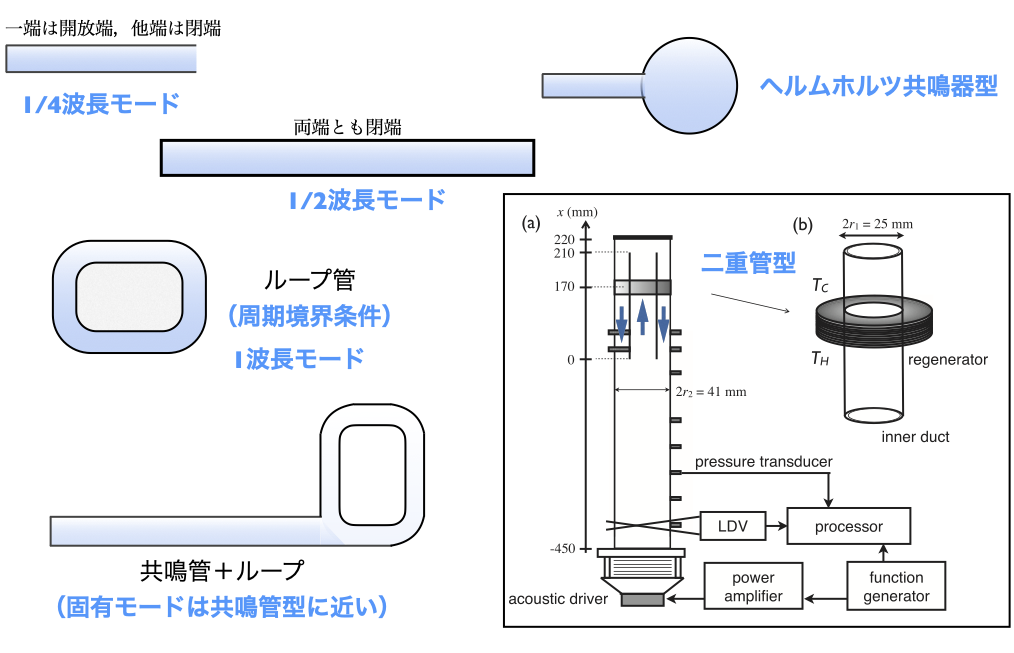
音波エンジンの基本形は共鳴管とループ管です.共鳴管は両端が開いているか閉じているかによって,固有モードが変わります.一端が閉じて他端が開いている場合には,基本固有モードの振動では,閉端で圧力の腹(流速の節),開端で圧力の節(流速の腹)ができます.両端が閉じている場合には,両端で圧力の腹(流速の節),中央で圧力の節(流速の腹)が形成されます.ループ管の基本モードはループ一周が波長に等しくなるようなモードです.
共鳴管とループ管を組み合わせたタイプもありますし,同軸二重管を使ったタイプもあります.八の字型などのバリエーションも検討されているようです.
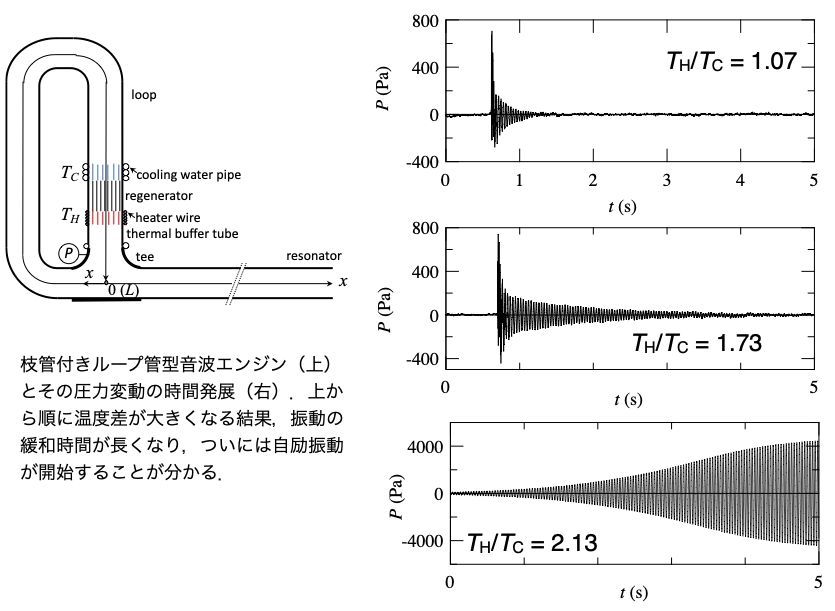
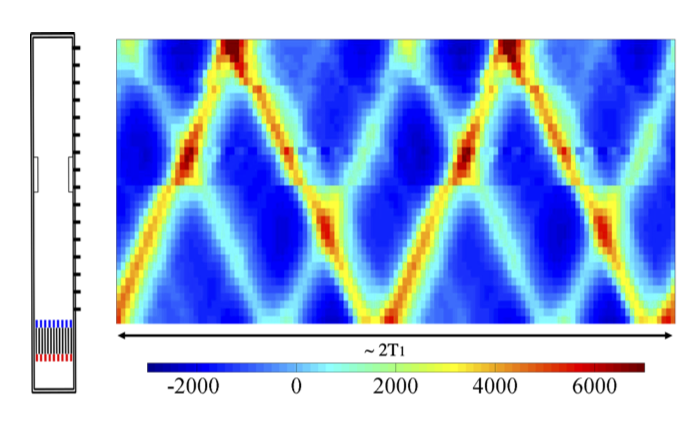
外部から加える熱量を増やすと,音波エンジンはひとりでに固有モードで振動を開始します.たしかに不思議な現象に感じます.どのようにして発振に至るかを見るために,温度差が十分に高くないときになにが起こるかを検討した例があります.下の図を見てください.
音波エンジンに外部から刺激を加えたとします.開放端を持つ音波エンジンならスピーカーで音を発生させてもよいし,手のひらで開放端を(鼓を打つように)叩いてもよいです.そうすると固有モードの音響振動が一時的に発生しますが,時間が経つとやがて静止状態に至ります.
音波エンジンに加える熱量を増した状態で同じことをして見ると,先ほどと同じくやがて振動は止まりますが,止まるまでの時間が長くなることがわかります.さらに加熱量をますと,ついには静止せずに振動し続けるようになります.このときの温度が発振開始温度になります.この温度では,外部から意図的に刺激を加えなくても自然のゆらぎが勝手に成長して定常振動に至ります.
原動機として考えると,高温部と低温部の温度比は大きい方が本質的に効率が高いのですが,温度比が小さくても動作可能です.音波エンジンの場合は,複数の蓄熱器を使ったり,作動気体に水を混ぜたりすることで動作温度がかなり小さくなることが知られています.低温部が室温程度のとき,100度を下回るような高温部温度でも振動が開始することもあります.
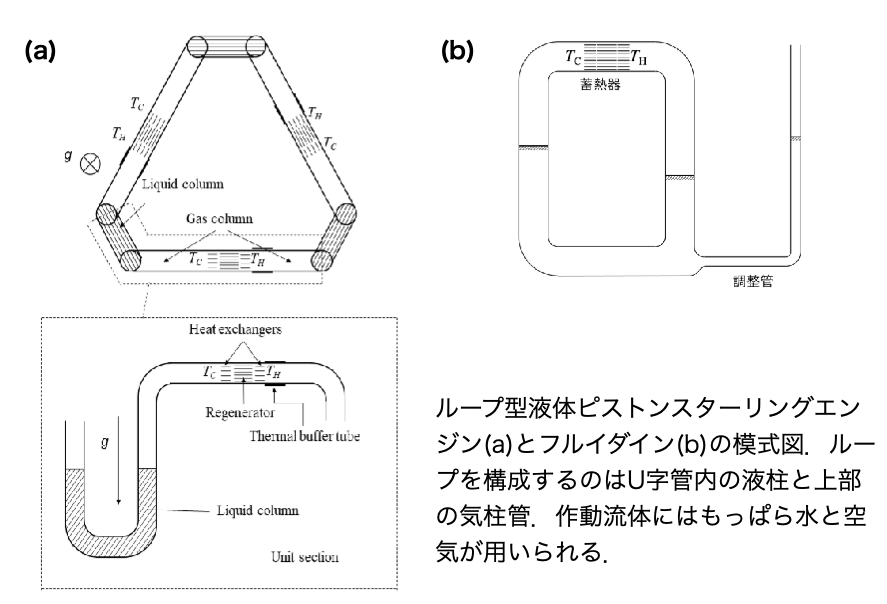
音波エンジンの共鳴器としてU字管内の液柱を使う場合も振動発生に必要な温度差が低くなることが知られています. このタイプの装置は液体ピストンスターリングエンジンと呼ばれます. 複数のU字管をリング上に結合した装置や,U字管と調整管を組み合わせた装置(フルイダイン)があります.
音波エンジンや音波クーラーの実用化に向けて世界中で努力が続けられています.その用途は,フロンを利用しない保冷庫,産業排熱用ヒートポンプ,天然ガス液化用冷凍機など様々です.
可動部品を必要としないことや簡単構造であることから,長寿命なことが最大の特徴です.一見ローテクに見えてハイテクなのが面白い点です.簡単構造だから作るのも簡単だし,もし壊れた時にも簡単に修理できます.そのような特徴を最大限に発揮できるような用途の開発も重要な研究課題です.
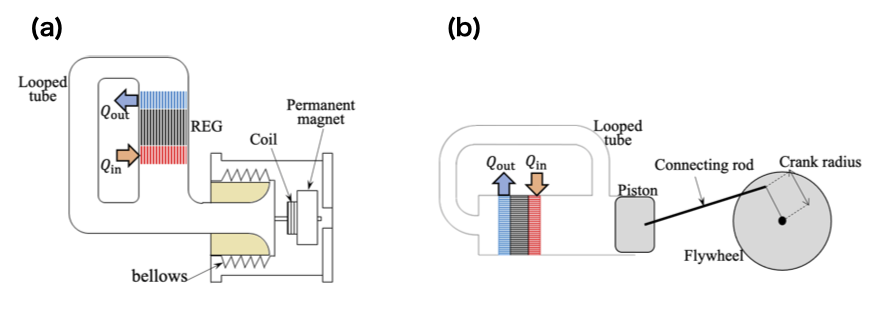
音波エンジンを発電機にする方法にはいくつかあります. 代表的なのは直動発電機 (リニアオルタネータ)と組み合わせる方法です. この方法では,熱で発生した音響振動でリニアオルタネータのコイルもしくはマグネットを往復振動させ,電磁誘導の原理で発電を行います. このときの音響振動の周波数は,音波エンジンとリニアオルタネータで構成される系の固有振動数です. 互いの周波数特性を考慮した上で組み合わせを考える必要があります.
最近では,リニアオルタネータの代わりに回転式発電機を用いることも可能になってきました. その場合,クランク機構を用いて作動気体の振動運動を回転運動に変換してから発電機に接続する方法と,双方向式タービンを用いて振動運動を回転運動に変換する方法があります.
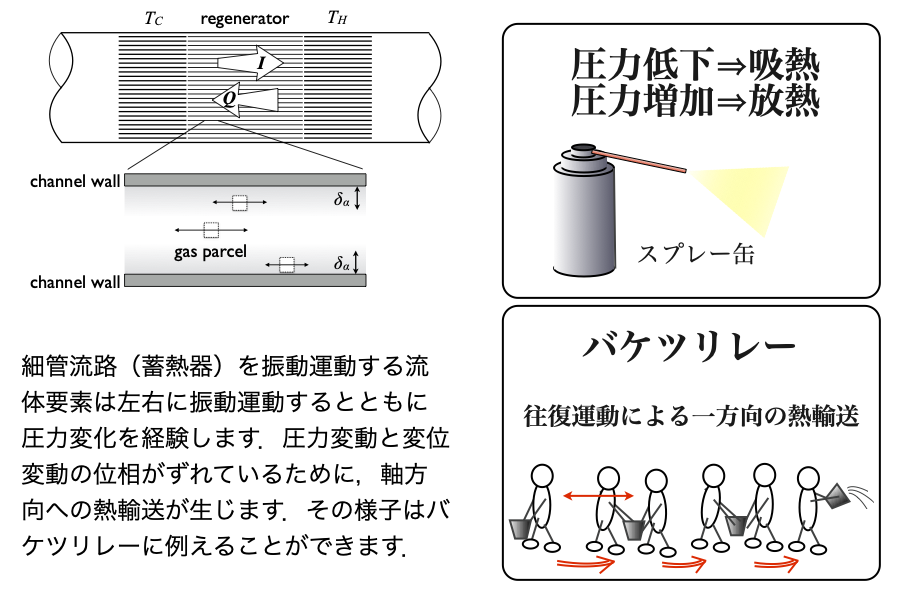
気体は圧力変化に応じて吸放熱する性質があります. 少し例は違いますが,殺虫剤やヘアスプレーなどのスプレー缶を使うときを思い出してください. 噴射すると缶が冷たくなることに気付いた人はいるでしょう.これが圧力低下に伴う吸熱作用の一例です. 逆に圧力が増加すると発熱する性質があります. 音波では作動気体の圧力は時間的に上昇と低下を繰り返しますから,そのおかげで冷却作用が起こると思うかもしれません. しかし,圧力変化だけでは不十分です. 大事なのは圧力変化に位置変動をうまく組み合わせることです. なぜなら,気体が同じ場所にいたまま吸放熱を繰り返したとしてもその場で吸熱,放熱をするだけで,一方向への熱輸送は起こらないからです.
位置変動と圧力変動が適切な位相差で起こることにより,低温側に移動したときに吸熱,高温側に移動したときに放熱を繰り返すことで低温から高温への熱輸送が可能になります. この様子はバケツリレーにしばしば例えられます. 皆さんもたくさんの流路のなかの流体要素が整然とバケツリレーを行う様を思い浮かべてみてください.
スターリングエンジンも音波エンジンも作動気体の往復振動と圧力変動を組み合わせることで,熱力学サイクルを実行します. ランキンサイクルが循環流を用いて熱力学サイクルを実行することに対比させれば,スターリングエンジンも音波エンジンもどちらも振動流を用いた熱力学サイクルを実行する点で同じ種類に分類することができます. そのため,熱交換器や蓄熱器(再生器)のように共通の部品を持っています.
以前には,スターリングエンジンやピストンを持ち,音波エンジンはピストンを持たない,という言い方もできましたが,最近の音波エンジンにはピストンを持つものも出てきました. スターリングエンジンも音波エンジンも同じ振動流型熱機関として捉え直せば,両方の長所を兼ね備えたハイブリッドも生まれるかもしれません. 相違点だけでなく類似点に着目することで新しい展開が生まれる可能性があります.
興味深い質問です. 音波エンジンやクーラーは確かに画期的なエネルギー変換技術です. 音波を発生するエンジンや音波で冷却するクーラーは最近の技術ですが,熱から動力を生み出すことや動力を使って冷却を実現する技術はすでに実用化され,しかも100年以上の長い歴史を持っています. そのため,音波エンジンや音波クーラーの出力や効率が増加したとしても,それだけでは現在のエネルギー変換技術に置き換わることにはならないと想像しています.
熱音響が実用化されるには,この技術の持つ特徴を最大限に発揮できる用途の開発が第一歩と思います. たとえばインフラ設備が不十分な環境では,簡単構造に由来する長期信頼性や維持管理の容易さは重要な価値を持つはずです. 具体的なニーズについて民間企業の方々と意見交換したいと思っています.お声がけください.
音波エンジンの最近の話題の一つに同期現象や振動停止現象(oscillaton death)があります. 音波エンジンでは,十分に熱するとある一定の周波数の音響振動が生まれますが,その音波エンジンにスピーカーなどを使って別の周波数の振動を外部から作用させると,音波エンジンは周波数を外力に合わせてひとりでに調整します. これは同期現象と呼ばれます. また外力の代わりに,もう一つの音波エンジンを使用して,音波エンジン同士に相互作用させると,同期現象が起こるだけでなく,条件によってはどちらのエンジンも振動を完全に停止することもあります. これは振動停止現象と呼ばれます. 同期現象や振動停止現象は音波エンジンだけでなく生体を含む多様な系で観測される普遍的な現象ですが,とくに音波エンジンの場合は周波数調整のための方法や,ガスタービンエンジンなどにおける迷惑な燃焼振動の抑制のための方法に活用できる可能性があります.
参考になる本や解説論文はありますか?
熱音響に関する書籍を探すならまずは富永昭氏の教科書です.英語ですがSwiftの教科書も入手可能です.最近発行された書籍もあります. 優れた解説論文もあります.
教科書
富永昭:熱音響工学の基礎,内田老鶴圃,(1998).G. W. Swift: Thermoacoustics -A unifying perspective for some engines and refrigerators-, Acoustical Society of America, (2002).
熱音響を勉強するなら誰でもよむ本.
琵琶哲志:熱音響デバイス,コロナ社.
T. Biwa: Introduction to Thermoacoustic Devices, World Scientific (2021).
最近出版されました.
レビュー
A. Tominaga, “Thermodynamic aspects of thermoacoustic theory,” Cryogenics, 35 427–440 (1995).G. W. Swift, “Thermoacoustic engines,” J. Acoust. Soc. Am, 84, 1145–1180 (1988).
熱音響を勉強するならまずこの2本を読む.
S. L. Garrett, “Thermoacoustic engines and refrigerators,” Am. J. Phys., 72, 11–17 (2004).
熱音響に関する長大な文献リスト(106本)あり.
解説論文
井上龍夫,河野新,“熱音響理論の図示化による理解”,低温工学,29, 558–567 (1994).みんなこれで熱音響理論の勉強を始めた.
井上龍夫,“熱音響機器のイメージと分類案”,低温工学,43, 577–581 (2008).
矢崎太一,“音の新展開:音の熱機関”,応用物理,75, 1345–1348 (2006).
矢崎太一,上田祐樹,琵琶哲志,“音を利用して冷やす方法:熱音響冷凍機の原理と試作”,日本音響学会誌,62, 128–133 (2006).
矢崎太一,“細管内の音波伝播と熱音響現象”,Journal of Japan Society of Fluid Mechanics, 24, 395–404 (2005).
熱音響の歴史も含めて書かれている.
矢崎太一,“熱音響エンジンと冷凍機 —Why and How?”,機械の研究,54, 1207–1216 (2002).
琵琶哲志,“熱音響効果とその冷凍への応用”,冷凍,77, 240–246 (2002).
琵琶哲志,“熱音響冷凍”,冷凍, 79, 874–881 (2004).
S. L. Garrett and S. Backhaus, “The power of sound”, American Scientist, 88, 516–525 (2000).
富永昭,パリティ,14, 26–28 (1999).
G. W. Swift, “Thermoacoustic engines and refrigerators,” Physics Today, 48, 22–28 (1995).
J. Wheatley, T. Hofler, G. W. Swift, A. Migliori, “Understanding some simple phenomena in thermoacoustics with applications to acoustical heat engines,” Am. J. Phys. 53 147–162 (1984).
杉本信正,“熱流の不安定性と熱音響現象 第1回 導入編“,ながれ,33, 181–194 (2014).
杉本信正,“熱流の不安定性と熱音響現象 第2回 線形理論編“,ながれ,33, 307–322 (2014).
杉本信正,“熱流の不安定性と熱音響現象 第3回 非線形現象編“,ながれ,33, 375–393 (2014).
流体力学を専門とする理論的研究者による解説.